Search
Close
Search
Advanced Search
Search Menu

Abstract

The correlation between alleles at a pair of genetic loci is a measure of linkage disequilibrium. The square of the sample correlation multiplied by sample size provides the usual test statistic for the hypothesis of no disequilibrium for loci with two alleles and this relation has proved useful for study design and marker selection. Nevertheless, this relation holds only in a diallelic case, and an extension to multiple alleles has not been made. Here we introduce a similar statistic, R2, which leads to a correlation-based test for loci with multiple alleles: for a pair of loci with k and m alleles, and a sample of n individuals, the approximate distribution of n(k – 1)(m – 1)/(km)R2 under independence between loci is

\(\mathrm{{\chi}}_{(k{-}1)(m{-}1)}^{2}\)
⁠. One advantage of this statistic is that it can be interpreted as the total correlation between a pair of loci. When the phase of two-locus genotypes is known, the approach is equivalent to a test for the overall correlation between rows and columns in a contingency table. In the phase-known case, R2 is the sum of the squared sample correlations for all km 2 × 2 subtables formed by collapsing to one allele vs. the rest at each locus. We examine the approximate distribution under the null of independence for R2 and report its close agreement with the exact distribution obtained by permutation. The test for independence using R2 is a strong competitor to approaches such as Pearson's chi square, Fisher's exact test, and a test based on Cressie and Read's power divergence statistic. We combine this approach with our previous composite-disequilibrium measures to address the case when the genotypic phase is unknown. Calculation of the new multiallele test statistic and its P-value is very simple and utilizes the approximate distribution of R2. We provide a computer program that evaluates approximate as well as “exact” permutational P-values.

THE phenomenon of nonrandom co-occurrence of alleles at two loci on the same haplotype is known as linkage disequilibrium (LD). It is an important population genetic concept with wide applications including theoretical studies of evolutionary dynamics (Lewontin 1974), forensic science (Evett and Weir 1998), conservation genetics and studies of effective population size (Waples 2006), evolutionary history, and human origins (Tishkoff  et al. 1996). The extent of LD in populations has been of great interest since the development of molecular techniques allowing genotypes to be obtained at multiple loci throughout the genome. Characterization of LD in human populations has been instrumental in fine mapping of complex genetic traits in both candidate gene and whole-genome association designs. Although diallelic loci (SNPs) are utilized in most association studies, multiallelic markers (microsatellites or SNP haplotypes) will continue to be useful in genetic research, most prominently in forensic applications and studies of population size and history. Multiallelic loci provide greater precision and may yield higher power to detect and characterize LD. A simulation study by Slatkin (1994) reported an increase in power with the number of alleles to detect LD by Fisher's exact test under a finite-allele mutation model with drift and recombination. More generally, power is not a simple function of the number of alleles, as it depends on the actual disequilibria and allelic frequencies (Weir and Cockerham 1978). Formally, the LD coefficient for alleles A and B at loci A and B refers to the deviation of the joint frequency, gametic or haplotypic, from the product of allele frequencies DAB = pAB – pApB. The correlation between alleles is defined as
\[\mathrm{{\rho}}_{AB}{=}\frac{D_{AB}}{\sqrt{p_{A}(1{-}p_{A})p_{B}(1{-}p_{B})}}.\]
Strictly speaking, the correlation is for the indicator variables xA and yB that equal 1 when the alleles are A and B and zero otherwise. This correlation coefficient has drawn much attention during recent years because the quantity
\(X_{AB}^{2}{=}nr_{AB}^{2}\)
⁠, where rAB is the value of ρAB in a sample of n gametes, is asymptotically distributed as
\(\mathrm{{\chi}}_{(1)}^{2}\)
under the hypothesis that ρAB = 0. This relation has obvious implications for issues of power of association studies and strategies for selecting subsets of genetic markers representative of common haplotypes for genomewide analysis (Pritchard and Przeworski 2001; International  Hapmap  Consortium 2003; Terwilliger and Hiekkalinna 2006). However, no similar relation has been proposed for markers with more than two alleles at each locus. There is a statistical difficulty in that, beyond the two-allele case, the total squared correlation R2 does not have a limiting chi-square distribution. Briefly, a sum of squared normal variables,
\({\sum}Z_{i}^{2}\)
⁠, has a χ2-distribution only when the variance–covariance matrix of the Zi's is a projection matrix. A more general result is usually stated in the matrix notation, regarding the distribution of a quadratic form, Z′CZ (Searle 1971, Chap. 2, Theorem 2). In our case, C is an identity matrix. Pearson's X2-statistic is an example of such a sum, while the sum of squared LD correlations is not. Thus, despite the vast theory on contingency tables, the distribution of R2 has not been adopted for testing interactions. Nevertheless, different approximations by a scaled chi-square distribution are possible for a sum of dependent chi-squares (e.g., Box 1954). Here we report a very simply computed chi-square approximation that appears to have good properties. This result is further applied to testing LD at a pair of multiallelic loci when only single-locus genotypes are scored unambiguously. Earlier work on characterization and testing of LD at a pair of multiallelic loci includes accounts by Hill (1975); Yamazaki (1977); Weir and Cockerham (1978); Weir (1979); Karlin and Piazza (1981); Hedrick (1987); Zaykin  et al. (1995); Kalinowski and Hedrick (2000); Zapata (2000); Schaid (2004); and Zhao  et al. (2005, 2007). Similar to the methods of Weir (1979) and Schaid (2004), our correlation LD approach is based on the composite disequilibrium definition. The composite disequilibrium approach has certain desirable properties. It is robust with respect to single-locus deviations from Hardy–Weinberg equilibrium (HWE). The composite disequilibrium coefficient is estimated directly from genotypic counts, and thus it is readily computed from data with the unknown gametic phase. Earlier work (Weir 1979; Schaid 2004; Zaykin 2004) demonstrated good statistical properties associated with this approach.

The correlation LD test is recommended for usage and can be readily applied for screening large numbers of pairs of multiallelic loci. It is also applicable for conducting correlation-based tests for interaction in contingency tables. Our program provides exact (permutational) P-values for tests based on R2.

METHODS

Known gametic phase:

When the gametic phase is unambiguous, the two-locus haplotype observations can be arranged into a k × m contingency table with the sample size N being equal to twice the number of individuals n, N = 2n. The cell counts in the table represent N haplotype observations: the (i, j)th cell has the number nij of haplotypes carrying allele i at the first locus and allele j at the second. We assume multinomial sampling of haplotypes. The observed haplotype frequencies are
\({\tilde{p}}_{ij}{=}n_{ij}/N\)
⁠. Row and column frequencies for the table of haplotype frequencies correspond to the vectors of allele frequencies at the two loci: {p1, … , pk} and {q1, … , qm}. The observed correlation for the cell (i, j) is
\[r_{ij}{=}\frac{{\tilde{p}}_{ij}{-}{\tilde{p}}_{i}{\tilde{q}}_{j}}{\sqrt{{\tilde{p}}_{i}(1{-}{\tilde{p}}_{i}){\tilde{q}}_{j}(1{-}{\tilde{q}}_{i})}}.\]
(1)
We propose the following two correlation-based statistics, both having an approximate chi-square distribution (as shown in  appendix a). The eigenvalue-based statistic is
\[T_{1}{=}\frac{N{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}r_{ij}^{2}}{\mathrm{{\sigma}}}{\mathrm{{\sim}}^{\mathrm{app}}}\mathrm{{\chi}}_{(d)}^{2},\]
(2)
where
\[\mathrm{{\sigma}}{=}\frac{\mathrm{trace}(\mathbf{\mathrm{V}}_{R}\mathbf{\mathrm{V}}_{R})}{km}\]
\[d{=}\frac{(km)^{2}}{\mathrm{trace}(\mathbf{\mathrm{V}}_{R}\mathbf{\mathrm{V}}_{R})}.\]
The statistic T2 is much simpler, as it does not involve a computation of eigenvalues:
\[T_{2}{=}\frac{(k{-}1)(m{-}1)N}{km}{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}r_{ij}^{2}{\mathrm{{\sim}}^{\mathrm{app}}}\mathrm{{\chi}}_{(k{-}1)(m{-}1)}^{2}.\]
(3)

Unknown haplotype phase:

Scoring genotypes one locus at a time creates ambiguity in determining pairs of haplotypes in individuals that are heterozygous at both loci. A maximum-likelihood solution for obtaining sample haplotype frequencies was suggested by Hill (1974, 1975) and elaborated on by Weir and Cockerham (1979). This approach was extended to multiple loci (Excoffier and Slatkin 1995) with the use of the EM algorithm incorporating the likelihood under the assumption of HWE. Weir (1979) sought to avoid making the HWE assumption and suggested estimating the composite disequilibrium defined as ΔAB = pAB + pA/B − 2pApB, where pA/B is the joint frequency of alleles A and B at two different gametes within individuals. The corresponding composite LD correlation is
\[\mathrm{{\rho}}_{AB}^{\mathrm{c}}{=}\frac{{\Delta}_{AB}}{\sqrt{{[}p_{A}(1{-}p_{A}){+}D_{A}{]}{[}p_{B}(1{-}p_{B}){+}D_{B}{]}}},\]
(4)
where DA, DB are the the Hardy–Weinberg disequilibrium coefficients at the two loci. Strictly speaking, this is the correlation of the number of A and B alleles carried by an individual (Weir 1979; Zaykin 2004). The composite coefficient is directly estimated from two-locus counts by simple counting (Weir 1979). Under HWE, the intergametic disequilibrium term DA/B = pA/B − pApB = 0, and the population value of ΔAB = DAB.
The composite correlations for a pair of alleles in a multiple-allele system are
\[\mathrm{{\rho}}_{ij}^{\mathrm{c}}{=}\frac{{\Delta}_{ij}}{\sqrt{{[}p_{i}(1{-}p_{i}){+}D_{i}{]}{[}q_{j}(1{-}q_{j}){+}D_{j}{]}}}.\]
Weir and Cockerham (1989) gave a decomposition of the two-locus genotype frequency
\(P_{AB}^{AB}\)
as a sum of functions of allele frequencies and two-locus disequilibria. Writing out the two-locus analog of the Hardy–Weinberg disequilibrium (HWD),
\(P_{AB}^{AB}{-}p_{AB}^{2}\)
⁠, in these terms shows that under the two-locus HWE, only the DAB and thus ΔAB disequilibria are nonzero. Therefore, assuming two-locus HWE, a chi-square statistic for testing LD can be written as
\[(X^{\mathrm{c}})_{AB}^{2}{=}n{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}\frac{\mathrm{{\tilde{{\Delta}}}}_{ij}^{2}}{{\tilde{p}}_{i}{\tilde{q}}_{j}},\]
(5)
as was suggested by Weir (1979). Under HWE, the composite coefficient estimates the usual LD. On the basis of Fisher's formula for approximate variances, Schaid (2004) derived the covariance matrix of the sample LD coefficients (W). He proposed a chi-square test based on a quadratic form. The test statistic definition involves a generalized inverse, W−. This test is analogous to (19). For the vector containing all sample composite LD coefficients
\(\mathbf{\mathrm{{\Delta}}}^{T}{=}{\{}\mathrm{{\hat{{\Delta}}}}_{ij}{\}}\)
⁠, Schaid's test statistic,
\(S^{2}{=}\mathbf{\mathrm{{\Delta}}}^{T}\mathbf{\mathrm{W}}^{{-}}\mathbf{\mathrm{{\Delta}}}\)
⁠, has an asymptotic chi-square distribution with the degrees of freedom equal to the rank of W. Schaid's test explicitly incorporates deviations from HWE.
We base the unknown-phase extension of the correlation LD approach on the approximate sampling distribution of the total composite LD correlation,
\begin{eqnarray*}&&(R^{\mathrm{c}})^{2}{=}{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}(r^{\mathrm{c}})_{ij}^{2}\\&&{=}{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}\frac{\mathrm{{\hat{{\Delta}}}}_{ij}^{2}}{{[}{\tilde{p}}_{i}(1{-}{\tilde{p}}_{i}){+}{\tilde{D}}_{i}{]}{[}{\tilde{q}}_{j}(1{-}{\tilde{q}}_{j}){+}{\tilde{D}}_{j}{]}},\end{eqnarray*}
(6)
where
\((r^{\mathrm{c}})_{ij}^{2}\)
denotes sample values of
\((\mathrm{{\rho}}^{\mathrm{c}})_{ij}^{2}\)
⁠. Comparing this statistic to (5) shows that now the deviations from HWE at both loci are explicitly incorporated into the test.
Schaid's test statistic as well as (Rc)2 assumes that trigenic and quadrigenic two-locus disequilibria can be ignored. These disequilibria compare joint frequencies of three and four alleles at two loci with the products of allele frequencies, after removing any lower-order disequilibria (Weir 1996). To obtain the Box-type approximation (for the statistic T1), the elements of the matrix W are scaled as
\({\{}W_{ij}/\sqrt{W_{ii}W_{jj}}{\}}\)
⁠. This gives the correlation matrix WR. As before, the scale parameter is
\(\mathrm{{\sigma}}{=}\mathrm{trace}(\mathbf{\mathrm{W}}_{R}\mathbf{\mathrm{W}}_{R})/(km)\)
⁠, and the degrees of freedom are
\(d{=}(km)^{2}/\mathrm{trace}(\mathbf{\mathrm{W}}_{R}\mathbf{\mathrm{W}}_{R})\)
⁠. Then the two statistics with their approximate distributions are
\[T_{1}{=}\frac{n(R^{\mathrm{c}})^{2}}{\mathrm{{\sigma}}}{\mathrm{{\sim}}^{\mathrm{app}}}\mathrm{{\chi}}_{(d)}^{2}\]
(7)
\[T_{2}{=}\frac{(k{-}1)(m{-}1)}{km}n(R^{\mathrm{c}})^{2}{=}(k{-}1)(m{-}1)n{\bar{r}}^{2}{\mathrm{{\sim}}^{\mathrm{app}}}\mathrm{{\chi}}_{(k{-}1)(m{-}1)}^{2},\]
(8)
where
\({\bar{r}}^{2}{=}(R^{\mathrm{c}})^{2}/(km)\)
is the average composite correlation.

Type-I error rates, goodness of fit to the null distribution, and power:

A common way to evaluate a test performance under the null hypothesis is to report the type-I error, or the proportion of P-values that fall below a rejection threshold, such as α = 0.05. An empirical estimate of the type-I error is that proportion in a large number of simulations conducted under the null hypothesis. We denote the number of simulations by B. For a more complete evaluation of the P-value distribution produced by a test, we propose to compute a statistic SB that adds up the squares of deviations of ordered P-values from the respective theoretical values expected under the null distribution. A visual method of plotting ordered P-values against the corresponding expected values of order statistics is known as a “rankit plot” (Ipsen and Jerne 1944). Such a plot very closely corresponds to the common “Q-Q” plot (where values are plotted against quantiles instead), unless the value of B is small. The deviation from the null by visual inspection is judged by the deviation of actual P-values from the expected straight line. The essence of the statistic SB is to capture the extent of this deviation. Since the usual type-I error reports the proportion of P-values below a single fixed cutoff point (a nominal level), commonly chosen to be 5%, it is possible that there would be a different degree of closeness to the nominal value at a different cutoff point. In contrast, the statistic SB has an advantage in that it gives a summary of the correspondence of P-values with the null distribution for the entire (0, 1) interval.

We denote the ordered set of P-values obtained from B simulations as
\({\{}p_{(1)},{\ldots},p_{(B)}{\}}\)
⁠. The random variable that corresponds to the observed p(i) is denoted by P(i). The summary statistic measuring the lack of fit to the null distribution is
\[S_{B}{=}\sqrt{\frac{1}{B}{{\sum}_{i{=}1}^{B}}{[}p_{(i)}{-}\mathcal{E}(P_{(i)}){]}^{2}}.\]
(9)
Under the null hypothesis, the distribution of the order statistics P(i) would be Beta(i, B – i + 1) if the distribution of the test statistic was continuous and exact, rather than approximate. The computational formula for SB is
\[S_{B}{=}\sqrt{\frac{1}{B}{{\sum}_{i{=}1}^{B}}\left[p_{(i)}{-}\frac{i}{B{+}1}\right]^{2}}.\]
(10)
Larger values of SB indicate larger deviations from the null distribution. When P-values indeed come from the null (uniform) distribution, we find the expected value of this statistic to be
\begin{eqnarray*}&&\mathcal{E}(S_{B}){\approx}\sqrt{\frac{1}{B}{{\sum}_{i{=}1}^{B}}\mathcal{E}{[}P_{(i)}{-}\mathcal{E}(P_{(i)}){]}^{2}}\\&&{=}\sqrt{\frac{1}{B}{{\sum}_{i{=}1}^{B}}\frac{i(B{-}i{+}1)}{(B{+}1)^{2}(B{+}2)}}\\&&{=}\sqrt{\frac{1}{6(1{+}B)}}.\end{eqnarray*}
(11)
Thus, for any test statistic, the fit of P-values to the uniform distribution can be simply evaluated by computing the proposed statistic, SB. We report and compare the values of SB for competing methods, in addition to the usual empirical type-I error rates.

Performance of the tests under the alternative hypothesis (HA) was characterized by statistical power. Power was estimated as the proportion of P-values that fall below the 5% rejection threshold, using data sets generated under HA.

RESULTS

Known haplotype phase:

The goal of this section is to compare performance of the proposed correlation-based tests. The performance was evaluated in terms of the classical type-I error and power. Additionally, the fit to the null distribution was evaluated with the usage of the coefficient SB, as described above. The following tests were used in this study:

  1. Correlation-based statistic T1 defined by (2).

  2. Correlation-based statistic T2 defined by (3).

  3. Cressie–Read's power divergence statistic,
    \[C^{\mathrm{{\lambda}}}{=}\frac{2}{\mathrm{{\lambda}}(\mathrm{{\lambda}}{+}1)}{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}n_{ij}\left\{\left(\frac{n_{ij}}{e_{ij}}\right)^{\mathrm{{\lambda}}}{-}1\right\}\]
    (12)
    with
    \(\mathrm{{\lambda}}{=}\frac{2}{3}\)
    (Cressie and Read 1984), where eij = ni·n·j/n are the expected counts. Cλ has an asymptotic chi-square distribution with (k – 1)(m – 1) d.f.
  4. Likelihood-ratio (LR) statistic,
    \[G^{2}{=}2{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}n_{ij}\mathrm{ln}(\frac{n_{ij}}{e_{ij}}){=}{\mathrm{lim}_{\mathrm{{\lambda}}{\rightarrow}0}}C^{\mathrm{{\lambda}}}.\]
    (13)
  5. Pearson's chi-square statistic,
    \[X^{2}{=}2{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}\frac{(n_{ij}{-}e_{ij})^{2}}{e_{ij}}{=}C^{1}.\]
    (14)

  6. Permutation-based tests using statistics as defined above, which we denote as Tp,

    \(G_{\mathrm{p}}^{2},{\,}C_{\mathrm{p}}^{\mathrm{{\lambda}}}\)
    ⁠, and X  
    \(_{\mathrm{p}}^{2}\)
    ⁠    . The statistics T1 and T2 correspond to the same permutational test, denoted by Tp.

  7. Fisher's exact test Fp, with the P-value approximated by a permutation test using the statistic

    \({\sum}_{i{=}1}^{k}{\sum}_{j{=}1}^{m}\mathrm{ln}(n_{ij}!)\)
    ⁠.

The P-value for a permutation test is defined as the proportion of times the test statistic computed from randomly sampled tables was found to be as extreme or more extreme than the statistic value for the original data. These random tables are generated with marginal counts constrained to be the same as that for the observed data set. We used K = 19,999 permutations to compute each P-value, and the number of simulations in all type-I error evaluation experiments was B = 100,000. Oden (1991) showed that the value of K in simulation experiments can be very much smaller than B. Boos and Zhang (2000) suggested that K can be as small as

\(8\sqrt{B}\)
⁠, and if the significance level is α, the value should preferably be such that (K + 1)α is an integer. The number of simulations to evaluate power was 10,000.

Tables 1–3 present results for the type-I error rates at the nominal 5% level and the closeness of fit to the null distribution as measured by the SB statistic. The tables of haplotype counts in this set of simulations have fixed margins and the cell counts are generated at random to satisfy the marginal conditions. A similar approach was used in the evaluation of small sample properties of some common tests, such as Pearson's chi square (e.g., Larntz 1978; Fienberg 1979). For example, the marginal frequencies in Table 2 are taken to be proportional to (2:3:5) for the rows and (2:3:4:5:6) for the columns. This matches the first setting of Table 6 in Larntz (1978). Our values for Pearson's X2 and the LR statistic G2 replicate the type-I error results of Larntz, who used sample sizes of 20–100. Across all simulations, our results confirm the previous observations (Larntz 1978) that the LR test (G2) has an inflated type-I error when sample sizes are small to moderate.

TABLE 1

Type-I error rates and values of the statistic measuring lack of fit to the null distribution, 1000 × SB for 3 × 5 tables: row margins, 5:3:2; column margins, 2:3:4:5:6

N
T2
T1
G2
C2/3
X2
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0370.0380.0510.0490.0510.0510.048
400.0470.0460.1030.0470.0450.0510.0510.0510.0510.051
600.0500.0490.0900.0500.0480.0520.0510.0510.0510.052
800.0490.0480.0800.0490.0470.0500.0510.0500.0500.051
1000.0490.0480.0730.0490.0470.0500.0500.0500.0490.049
10000.0510.0500.0520.0510.0510.0500.0510.0510.0510.051
1000 ×  SB
20555620078580.94171.12.128
40262812043301.511.51.41.3
6015177727181.31.31.31.41.4
8010125419131.31.61.51.51.5
1008.6104116110.570.680.480.530.56
1000
1
1.6
3.8
2.1
1.7
0.53
0.76
0.78
0.78
0.73
N
T2
T1
G2
C2/3
X2
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0370.0380.0510.0490.0510.0510.048
400.0470.0460.1030.0470.0450.0510.0510.0510.0510.051
600.0500.0490.0900.0500.0480.0520.0510.0510.0510.052
800.0490.0480.0800.0490.0470.0500.0510.0500.0500.051
1000.0490.0480.0730.0490.0470.0500.0500.0500.0490.049
10000.0510.0500.0520.0510.0510.0500.0510.0510.0510.051
1000 ×  SB
20555620078580.94171.12.128
40262812043301.511.51.41.3
6015177727181.31.31.31.41.4
8010125419131.31.61.51.51.5
1008.6104116110.570.680.480.530.56
1000
1
1.6
3.8
2.1
1.7
0.53
0.76
0.78
0.78
0.73

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 1

Type-I error rates and values of the statistic measuring lack of fit to the null distribution, 1000 × SB for 3 × 5 tables: row margins, 5:3:2; column margins, 2:3:4:5:6

N
T2
T1
G2
C2/3
X2
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0370.0380.0510.0490.0510.0510.048
400.0470.0460.1030.0470.0450.0510.0510.0510.0510.051
600.0500.0490.0900.0500.0480.0520.0510.0510.0510.052
800.0490.0480.0800.0490.0470.0500.0510.0500.0500.051
1000.0490.0480.0730.0490.0470.0500.0500.0500.0490.049
10000.0510.0500.0520.0510.0510.0500.0510.0510.0510.051
1000 ×  SB
20555620078580.94171.12.128
40262812043301.511.51.41.3
6015177727181.31.31.31.41.4
8010125419131.31.61.51.51.5
1008.6104116110.570.680.480.530.56
1000
1
1.6
3.8
2.1
1.7
0.53
0.76
0.78
0.78
0.73
N
T2
T1
G2
C2/3
X2
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0370.0380.0510.0490.0510.0510.048
400.0470.0460.1030.0470.0450.0510.0510.0510.0510.051
600.0500.0490.0900.0500.0480.0520.0510.0510.0510.052
800.0490.0480.0800.0490.0470.0500.0510.0500.0500.051
1000.0490.0480.0730.0490.0470.0500.0500.0500.0490.049
10000.0510.0500.0520.0510.0510.0500.0510.0510.0510.051
1000 ×  SB
20555620078580.94171.12.128
40262812043301.511.51.41.3
6015177727181.31.31.31.41.4
8010125419131.31.61.51.51.5
1008.6104116110.570.680.480.530.56
1000
1
1.6
3.8
2.1
1.7
0.53
0.76
0.78
0.78
0.73

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 2

Type-I error rates and values of the statistic measuring lack of fit to the null distribution, 1000 × SB for 3 × 5 tables: row margins, 2:3:5; column margins, 2:3:4:5:6

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0360.0380.0510.0480.0510.0510.044
400.0460.0440.1000.0450.0430.0490.0490.0490.0500.049
600.0490.0470.0880.0490.0460.0500.0510.0500.0500.050
800.0490.0480.0790.0500.0470.0500.0500.0500.0500.050
1000.0490.0470.0720.0490.0470.0490.0490.0500.0490.049
10000.0510.0500.0510.0500.0500.0500.0500.0500.0500.050
1000 × SB
20555720078590.82130.861.623
40262712042290.851.50.850.871.9
6017187928200.671.21.10.910.93
8011135420131.11.31.21.21.2
1009.1114216120.660.910.840.770.81
1000
1.7
1
3
1.2
0.81
0.77
0.78
0.76
0.76
0.75
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0360.0380.0510.0480.0510.0510.044
400.0460.0440.1000.0450.0430.0490.0490.0490.0500.049
600.0490.0470.0880.0490.0460.0500.0510.0500.0500.050
800.0490.0480.0790.0500.0470.0500.0500.0500.0500.050
1000.0490.0470.0720.0490.0470.0490.0490.0500.0490.049
10000.0510.0500.0510.0500.0500.0500.0500.0500.0500.050
1000 × SB
20555720078590.82130.861.623
40262712042290.851.50.850.871.9
6017187928200.671.21.10.910.93
8011135420131.11.31.21.21.2
1009.1114216120.660.910.840.770.81
1000
1.7
1
3
1.2
0.81
0.77
0.78
0.76
0.76
0.75

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 2

Type-I error rates and values of the statistic measuring lack of fit to the null distribution, 1000 × SB for 3 × 5 tables: row margins, 2:3:5; column margins, 2:3:4:5:6

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0360.0380.0510.0480.0510.0510.044
400.0460.0440.1000.0450.0430.0490.0490.0490.0500.049
600.0490.0470.0880.0490.0460.0500.0510.0500.0500.050
800.0490.0480.0790.0500.0470.0500.0500.0500.0500.050
1000.0490.0470.0720.0490.0470.0490.0490.0500.0490.049
10000.0510.0500.0510.0500.0500.0500.0500.0500.0500.050
1000 × SB
20555720078590.82130.861.623
40262712042290.851.50.850.871.9
6017187928200.671.21.10.910.93
8011135420131.11.31.21.21.2
1009.1114216120.660.910.840.770.81
1000
1.7
1
3
1.2
0.81
0.77
0.78
0.76
0.76
0.75
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0410.0390.1190.0360.0380.0510.0480.0510.0510.044
400.0460.0440.1000.0450.0430.0490.0490.0490.0500.049
600.0490.0470.0880.0490.0460.0500.0510.0500.0500.050
800.0490.0480.0790.0500.0470.0500.0500.0500.0500.050
1000.0490.0470.0720.0490.0470.0490.0490.0500.0490.049
10000.0510.0500.0510.0500.0500.0500.0500.0500.0500.050
1000 × SB
20555720078590.82130.861.623
40262712042290.851.50.850.871.9
6017187928200.671.21.10.910.93
8011135420131.11.31.21.21.2
1009.1114216120.660.910.840.770.81
1000
1.7
1
3
1.2
0.81
0.77
0.78
0.76
0.76
0.75

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 3

Type-I error rates and values of the statistic measuring lack of fit to the null distribution, 1000 × SB for 5 × 7 tables: row margins, 2:3:4:5:6; column margins, 1:2:3:4:5:6:7

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0260.0260.0120.0060.0250.0490.0440.0490.0490.048
400.0380.0370.0780.0220.0360.0500.0500.0500.0500.050
600.0420.0420.1090.0320.0420.0500.0490.0500.0500.050
800.0450.0440.1170.0390.0440.0500.0490.0490.0500.049
1000.0460.0460.1120.0430.0450.0500.0500.0500.0500.050
10000.0510.0500.0570.0500.0500.0500.0500.0500.0500.050
1000 × SB
20989918084980.85320.811.368
40474818047480.563.30.470.545.9
60293019039310.550.620.650.650.89
80202117034221.51.91.61.51.7
100171815030181.21.31.11.11.2
1000
0.96
1.1
15
2
0.94
1.6
1.9
1.8
1.8
1.7
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0260.0260.0120.0060.0250.0490.0440.0490.0490.048
400.0380.0370.0780.0220.0360.0500.0500.0500.0500.050
600.0420.0420.1090.0320.0420.0500.0490.0500.0500.050
800.0450.0440.1170.0390.0440.0500.0490.0490.0500.049
1000.0460.0460.1120.0430.0450.0500.0500.0500.0500.050
10000.0510.0500.0570.0500.0500.0500.0500.0500.0500.050
1000 × SB
20989918084980.85320.811.368
40474818047480.563.30.470.545.9
60293019039310.550.620.650.650.89
80202117034221.51.91.61.51.7
100171815030181.21.31.11.11.2
1000
0.96
1.1
15
2
0.94
1.6
1.9
1.8
1.8
1.7

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 3

Type-I error rates and values of the statistic measuring lack of fit to the null distribution, 1000 × SB for 5 × 7 tables: row margins, 2:3:4:5:6; column margins, 1:2:3:4:5:6:7

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0260.0260.0120.0060.0250.0490.0440.0490.0490.048
400.0380.0370.0780.0220.0360.0500.0500.0500.0500.050
600.0420.0420.1090.0320.0420.0500.0490.0500.0500.050
800.0450.0440.1170.0390.0440.0500.0490.0490.0500.049
1000.0460.0460.1120.0430.0450.0500.0500.0500.0500.050
10000.0510.0500.0570.0500.0500.0500.0500.0500.0500.050
1000 × SB
20989918084980.85320.811.368
40474818047480.563.30.470.545.9
60293019039310.550.620.650.650.89
80202117034221.51.91.61.51.7
100171815030181.21.31.11.11.2
1000
0.96
1.1
15
2
0.94
1.6
1.9
1.8
1.8
1.7
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Type-I error
200.0260.0260.0120.0060.0250.0490.0440.0490.0490.048
400.0380.0370.0780.0220.0360.0500.0500.0500.0500.050
600.0420.0420.1090.0320.0420.0500.0490.0500.0500.050
800.0450.0440.1170.0390.0440.0500.0490.0490.0500.049
1000.0460.0460.1120.0430.0450.0500.0500.0500.0500.050
10000.0510.0500.0570.0500.0500.0500.0500.0500.0500.050
1000 × SB
20989918084980.85320.811.368
40474818047480.563.30.470.545.9
60293019039310.550.620.650.650.89
80202117034221.51.91.61.51.7
100171815030181.21.31.11.11.2
1000
0.96
1.1
15
2
0.94
1.6
1.9
1.8
1.8
1.7

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab

Both of the proposed statistics, T1 and T2 show a correct type-I error for the corresponding test. Moreover, examination of SB values indicates that small-to-moderate sample size behavior of these statistics is such that they provide the best fit to the null distribution among the asymptotic/approximate tests studied here. The simpler approximation, T2, shows the best fit.

Tables 4–7 present both power and the behavior under H0, given in terms of the type-I error and the SB values. The null distribution data sets corresponding to the power results were generated by randomly shuffling the data generated under the association model, to produce new counts under the hypothesis of no association. Sample sizes for different simulations are chosen depending on the strength of the population association, to provide intermediate to high power, and highlight the difference between the tests.

TABLE 4

Power and the corresponding H0 behavior for 4 × 3 tables at abs(D′) ± 0.5 (population parameters are defined in Table B1 of  appendix b)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5700.5540.5580.4070.3900.5750.5010.4660.4220.465
600.9080.9040.8900.8430.8330.9080.8460.8520.8440.842
Type-I error
300.0480.0450.0710.0380.0430.0510.0500.0510.0510.051
600.0500.0470.0800.0450.0440.0500.0490.0490.0490.050
1000 × SB
30323813051412.53.92.22.76.1
60
13
18
83
29
20
0.59
0.75
0.58
0.56
0.61
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5700.5540.5580.4070.3900.5750.5010.4660.4220.465
600.9080.9040.8900.8430.8330.9080.8460.8520.8440.842
Type-I error
300.0480.0450.0710.0380.0430.0510.0500.0510.0510.051
600.0500.0470.0800.0450.0440.0500.0490.0490.0490.050
1000 × SB
30323813051412.53.92.22.76.1
60
13
18
83
29
20
0.59
0.75
0.58
0.56
0.61

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 4

Power and the corresponding H0 behavior for 4 × 3 tables at abs(D′) ± 0.5 (population parameters are defined in Table B1 of  appendix b)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5700.5540.5580.4070.3900.5750.5010.4660.4220.465
600.9080.9040.8900.8430.8330.9080.8460.8520.8440.842
Type-I error
300.0480.0450.0710.0380.0430.0510.0500.0510.0510.051
600.0500.0470.0800.0450.0440.0500.0490.0490.0490.050
1000 × SB
30323813051412.53.92.22.76.1
60
13
18
83
29
20
0.59
0.75
0.58
0.56
0.61
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5700.5540.5580.4070.3900.5750.5010.4660.4220.465
600.9080.9040.8900.8430.8330.9080.8460.8520.8440.842
Type-I error
300.0480.0450.0710.0380.0430.0510.0500.0510.0510.051
600.0500.0470.0800.0450.0440.0500.0490.0490.0490.050
1000 × SB
30323813051412.53.92.22.76.1
60
13
18
83
29
20
0.59
0.75
0.58
0.56
0.61

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 5

Power and the corresponding H0 behavior for 4 × 3 tables at abs(D′) ± 0.5 (population parameters are defined in Table B2 of  appendix b)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5260.5100.4880.3420.3180.5290.4350.3970.3430.401
600.8920.8850.8640.7900.7710.8880.8230.8060.7820.795
Type-I error
300.0490.0450.0680.0380.0460.0500.0500.0510.0500.049
600.0520.0480.0720.0450.0470.0510.0510.0500.0500.051
1000 × SB
30293612044353.85.23.84.46.8
60
12
18
91
30
20
1.1
0.96
1
1.1
1.2
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5260.5100.4880.3420.3180.5290.4350.3970.3430.401
600.8920.8850.8640.7900.7710.8880.8230.8060.7820.795
Type-I error
300.0490.0450.0680.0380.0460.0500.0500.0510.0500.049
600.0520.0480.0720.0450.0470.0510.0510.0500.0500.051
1000 × SB
30293612044353.85.23.84.46.8
60
12
18
91
30
20
1.1
0.96
1
1.1
1.2

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 5

Power and the corresponding H0 behavior for 4 × 3 tables at abs(D′) ± 0.5 (population parameters are defined in Table B2 of  appendix b)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5260.5100.4880.3420.3180.5290.4350.3970.3430.401
600.8920.8850.8640.7900.7710.8880.8230.8060.7820.795
Type-I error
300.0490.0450.0680.0380.0460.0500.0500.0510.0500.049
600.0520.0480.0720.0450.0470.0510.0510.0500.0500.051
1000 × SB
30293612044353.85.23.84.46.8
60
12
18
91
30
20
1.1
0.96
1
1.1
1.2
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
300.5260.5100.4880.3420.3180.5290.4350.3970.3430.401
600.8920.8850.8640.7900.7710.8880.8230.8060.7820.795
Type-I error
300.0490.0450.0680.0380.0460.0500.0500.0510.0500.049
600.0520.0480.0720.0450.0470.0510.0510.0500.0500.051
1000 × SB
30293612044353.85.23.84.46.8
60
12
18
91
30
20
1.1
0.96
1
1.1
1.2

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 6

Power and the corresponding H0 behavior for 5 × 5 tables at abs(D′) ∈ (0.19–0.21) (population parameters are defined in Table B3 of  appendix b)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1500.7520.7490.7470.7190.7260.7540.6720.7230.7330.709
2000.8840.8820.8680.8620.8670.8840.8260.8630.8700.847
Type-I error
1500.0500.0480.0840.0480.0470.0500.0500.0500.0500.050
2000.0500.0490.0750.0500.0490.0500.0500.0510.0510.050
1000 × SB
1509.6117619122.11.92.22.42
200
5
6.4
52
12
6.8
1.3
0.88
1.2
1.3
1.2
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1500.7520.7490.7470.7190.7260.7540.6720.7230.7330.709
2000.8840.8820.8680.8620.8670.8840.8260.8630.8700.847
Type-I error
1500.0500.0480.0840.0480.0470.0500.0500.0500.0500.050
2000.0500.0490.0750.0500.0490.0500.0500.0510.0510.050
1000 × SB
1509.6117619122.11.92.22.42
200
5
6.4
52
12
6.8
1.3
0.88
1.2
1.3
1.2

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 6

Power and the corresponding H0 behavior for 5 × 5 tables at abs(D′) ∈ (0.19–0.21) (population parameters are defined in Table B3 of  appendix b)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1500.7520.7490.7470.7190.7260.7540.6720.7230.7330.709
2000.8840.8820.8680.8620.8670.8840.8260.8630.8700.847
Type-I error
1500.0500.0480.0840.0480.0470.0500.0500.0500.0500.050
2000.0500.0490.0750.0500.0490.0500.0500.0510.0510.050
1000 × SB
1509.6117619122.11.92.22.42
200
5
6.4
52
12
6.8
1.3
0.88
1.2
1.3
1.2
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1500.7520.7490.7470.7190.7260.7540.6720.7230.7330.709
2000.8840.8820.8680.8620.8670.8840.8260.8630.8700.847
Type-I error
1500.0500.0480.0840.0480.0470.0500.0500.0500.0500.050
2000.0500.0490.0750.0500.0490.0500.0500.0510.0510.050
1000 × SB
1509.6117619122.11.92.22.42
200
5
6.4
52
12
6.8
1.3
0.88
1.2
1.3
1.2

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 7

Power and the corresponding H0 behavior for the “sample heterogeneity” model (5 × 5 tables)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1000.6550.6550.6700.6580.6550.6570.6560.6580.6570.657
1500.8360.8350.8410.8350.8350.8360.8360.8360.8350.836
Type-I error
1000.0500.0500.0540.0500.0500.0500.0500.0500.0500.050
1500.0490.0490.0520.0490.0490.0490.0490.0490.0490.049
1000 × SB
1002.92.910431.21.11.21.21.1
150
2.9
2.9
8.3
3.8
2.9
1.6
1.7
1.6
1.6
1.7
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1000.6550.6550.6700.6580.6550.6570.6560.6580.6570.657
1500.8360.8350.8410.8350.8350.8360.8360.8360.8350.836
Type-I error
1000.0500.0500.0540.0500.0500.0500.0500.0500.0500.050
1500.0490.0490.0520.0490.0490.0490.0490.0490.0490.049
1000 × SB
1002.92.910431.21.11.21.21.1
150
2.9
2.9
8.3
3.8
2.9
1.6
1.7
1.6
1.6
1.7

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab
TABLE 7

Power and the corresponding H0 behavior for the “sample heterogeneity” model (5 × 5 tables)

N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1000.6550.6550.6700.6580.6550.6570.6560.6580.6570.657
1500.8360.8350.8410.8350.8350.8360.8360.8360.8350.836
Type-I error
1000.0500.0500.0540.0500.0500.0500.0500.0500.0500.050
1500.0490.0490.0520.0490.0490.0490.0490.0490.0490.049
1000 × SB
1002.92.910431.21.11.21.21.1
150
2.9
2.9
8.3
3.8
2.9
1.6
1.7
1.6
1.6
1.7
N
T2
T1
G2
C2/3
\(X^{2}\)
Tp
\(G_{\mathrm{p}}^{2}\)
\(C_{\mathrm{p}}^{2/3}\)
\(X_{\mathrm{p}}^{2}\)
Fp
Power
1000.6550.6550.6700.6580.6550.6570.6560.6580.6570.657
1500.8360.8350.8410.8350.8350.8360.8360.8360.8350.836
Type-I error
1000.0500.0500.0540.0500.0500.0500.0500.0500.0500.050
1500.0490.0490.0520.0490.0490.0490.0490.0490.0490.049
1000 × SB
1002.92.910431.21.11.21.21.1
150
2.9
2.9
8.3
3.8
2.9
1.6
1.7
1.6
1.6
1.7

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}100,000){]}}{=}1.29\)
⁠.

Open in new tab

The population association values for Tables 4–6 were generated as follows. The association value for the cell (i, j) can be measured in terms of LD, Dij = pij – piqj. The maximum absolute value of Dij is constrained by the marginal frequencies pi, qj and the association values for all cells were set as proportions of the maximum attainable value,

\(D{^\prime}_{ij}\)
(Lewontin 1964). The population frequencies, pij, and the values of
\(D{^\prime}_{ij}\)
are given in  appendix b, Tables B1–B3. Samples for each simulation experiment were obtained by multinomial sampling from these population frequencies. Both of the proposed tests (T1, T2) show type-I error rates close to the nominal 5% level. The simple approximation T2 shows the best fit to the null distribution among the asymptotic/approximate tests. Moreover, the power corresponding to T2 or its permutational equivalent Tp is somewhat higher than that for the rest of the tests. These differences in power are highly significant statistically, due to the paired nature of the data (P-values) and the large number of simulations.

As mentioned previously, in the known-phase case the test for LD is equivalent to a test for interaction in a contingency table. In principle, the tests based on the total correlation can be used in a classical setting of testing heterogeneity between several multinomial samples. Although a detailed examination of the proposed tests regarding this problem is beyond the scope of this article, a simulation study (Table 7) confirms that the proposed approach provides a competitive test. In the 5 × 5 tables used here, rows represent independent samples taken from five populations; and columns represent five categories (such as sample-specific allele frequencies). Population frequencies for each of the simulations were generated from the Dirichlet distribution with the common parameter, 20. A property of this sampling is such that the 1 and 99% population quantiles for the frequency of any of the five column categories are 0.1 and 0.3, with mean frequency 0.2. This range gives a measure of the between-population variability for each of the categories. Samples for each of the five populations were generated by multinomial sampling for each of the simulation runs. As before, data for the hypothesis of homogeneity (H0) were obtained by taking the sample generated as just described and reshuffling the counts under the constraints that the marginal frequencies of a particular sample are preserved. Table 7 shows good properties of the proposed tests under the hypothesis of no association. The power values are found to be identical to those provided by Fisher's exact test. The asymptotic version of the LR test (G2) shows a higher power; however, this value might be unreliable, because the type-I error of this test was found consistently inflated in all simulations.

Unknown haplotype phase:

This section gives results of the comparison between the two “LD correlation” statistics (T1, T2) and a chi-square test recently described by Schaid (2004), which has similarity in that it also utilizes the composite LD definition. Schaid's test (S2) corresponds to Pearson's chi-square in the “known-phase” case; however, there is no simple explicit expression for the test statistic in the ambiguous haplotype phase case. The calculation of S2 involves a generalized inverse of the covariance matrix of the sample composite LD. We assume a common scenario when single-locus genotypes are scored at each locus, without the knowledge about arrangement of the alleles on haplotypes across the loci.

The first set of simulations was designed for a two-locus linkage equilibrium system with five and seven alleles correspondingly. Both loci have high population levels of HWD. The amount of HWD and allele frequencies for various simulation settings are given in the legend to Table 8. The homozygote HWD values for the two loci (⁠

\(D{^\prime}_{ii}\)
⁠) are given as proportions of the maximum possible value. The heterozygote HW disequilibria are related to these as
\({\sum}_{i{\neq}j}D_{ij}{=}{\sum}_{i}D_{ii}/2\)
⁠. The simulation results confirm that both the correlation-based tests and Schaid's test are robust in the presence of high levels of population HWD. Similar to the known-phase results, the simple T2 approximation shows the best fit to the null distribution (under the hypothesis of linkage equilibrium).

TABLE 8

Type-I error and values of the statistic measuring lack of fit to the null distribution, 1000 × SB, for the composite LD tests: locus A, five alleles; locus B, seven alleles; n = 100

Setting
T2
T1
S2
Type-I error
I0.0500.0460.045
II0.0440.0430.043
III0.0500.0460.045
IV0.0510.0490.049
V0.0500.0490.048
1000 × SB
I12.215.215.8
II14.016.016.4
III8.211.611.2
IV8.010.110.9
V
5.2
5.8
6.1
Setting
T2
T1
S2
Type-I error
I0.0500.0460.045
II0.0440.0430.043
III0.0500.0460.045
IV0.0510.0490.049
V0.0500.0490.048
1000 × SB
I12.215.215.8
II14.016.016.4
III8.211.611.2
IV8.010.110.9
V
5.2
5.8
6.1

Setting I: locus A, pi, 0.15, 0.22, 0.15, 0.23, 0.25 and

\(D{^\prime}_{ii}\)
⁠, −1, 0.13, −1, 0.20, 0.12; locus B, qi, 0.16, 0.17, 0.11, 0.16, 0.16, 0.18, 0.05 and
\(D{^\prime}_{ii}\)
⁠, 0.10, 0.09, −1, 0.10, 0.10, 0.07, 1. Setting II: locus A, pi, 0.20, 0.18, 0.20, 0.20, 0.22 and
\(D{^\prime}_{ii}\)
⁠, 0.25, 1, 0.25, 0.25, 0.32; locus B, qi, 0.14, 0.14, 0.12, 0.16, 0.16, 0.14, 0.14 and
\(D{^\prime}_{ii}\)
⁠, 0.17, 0.17, 1, 0.23, 0.23, 0.17, 0.17. Setting III: locus A, pi, 0.18 0.18, 0.16, 0.24, 0.25 and
\(D{^\prime}_{ii}\)
⁠, −0.37, −0.37, −0.20, 0.24, 0.17; locus B, qi, 0.11, 0.15, 0.13, 0.14, 0.15, 0.16, 0.17 and
\(D{^\prime}_{ii}\)
⁠, 0.40, −0.31, −0.14, −0.19, 0.25, 0.22, 0.18. Setting IV: locus A, pi, 0.23, 0.38, 0.38 and
\(D{^\prime}_{ii}\)
⁠, 0.57, 0.68, 0.68; locus B, qi, 0.22, 0.25, 0.27, 0.27 and
\(D{^\prime}_{ii}\)
⁠, −0.35, −0.5, −0.56, −0.56. Setting V: locus A, pi, 0.32, 0.32, 0.35 and
\(D{^\prime}_{ii}\)
⁠, 0.60, 0.60, 0.48; locus B, qi, 0.26, 0.24, 0.24, 0.26 and
\(D{^\prime}_{ii}\)
⁠, 0.55, 0.67, 0.67, 0.55. Expected value of 1000 × SB for the uniform P-value distribution is
\(1000\sqrt{1/{[}6(1{+}10,000){]}}{=}4.08\)
⁠.

Open in new tab
TABLE 8

Type-I error and values of the statistic measuring lack of fit to the null distribution, 1000 × SB, for the composite LD tests: locus A, five alleles; locus B, seven alleles; n = 100

Setting
T2
T1
S2
Type-I error
I0.0500.0460.045
II0.0440.0430.043
III0.0500.0460.045
IV0.0510.0490.049
V0.0500.0490.048
1000 × SB
I12.215.215.8
II14.016.016.4
III8.211.611.2
IV8.010.110.9
V
5.2
5.8
6.1
Setting
T2
T1
S2
Type-I error
I0.0500.0460.045
II0.0440.0430.043
III0.0500.0460.045
IV0.0510.0490.049
V0.0500.0490.048
1000 × SB
I12.215.215.8
II14.016.016.4
III8.211.611.2
IV8.010.110.9
V
5.2
5.8
6.1

Setting I: locus A, pi, 0.15, 0.22, 0.15, 0.23, 0.25 and

\(D{^\prime}_{ii}\)
⁠, −1, 0.13, −1, 0.20, 0.12; locus B, qi, 0.16, 0.17, 0.11, 0.16, 0.16, 0.18, 0.05 and
\(D{^\prime}_{ii}\)
⁠, 0.10, 0.09, −1, 0.10, 0.10, 0.07, 1. Setting II: locus A, pi, 0.20, 0.18, 0.20, 0.20, 0.22 and
\(D{^\prime}_{ii}\)
⁠, 0.25, 1, 0.25, 0.25, 0.32; locus B, qi, 0.14, 0.14, 0.12, 0.16, 0.16, 0.14, 0.14 and
\(D{^\prime}_{ii}\)
⁠, 0.17, 0.17, 1, 0.23, 0.23, 0.17, 0.17. Setting III: locus A, pi, 0.18 0.18, 0.16, 0.24, 0.25 and
\(D{^\prime}_{ii}\)
⁠, −0.37, −0.37, −0.20, 0.24, 0.17; locus B, qi, 0.11, 0.15, 0.13, 0.14, 0.15, 0.16, 0.17 and
\(D{^\prime}_{ii}\)
⁠, 0.40, −0.31, −0.14, −0.19, 0.25, 0.22, 0.18. Setting IV: locus A, pi, 0.23, 0.38, 0.38 and
\(D{^\prime}_{ii}\)
⁠, 0.57, 0.68, 0.68; locus B, qi, 0.22, 0.25, 0.27, 0.27 and
\(D{^\prime}_{ii}\)
⁠, −0.35, −0.5, −0.56, −0.56. Setting V: locus A, pi, 0.32, 0.32, 0.35 and
\(D{^\prime}_{ii}\)
⁠, 0.60, 0.60, 0.48; locus B, qi, 0.26, 0.24, 0.24, 0.26 and
\(D{^\prime}_{ii}\)
⁠, 0.55, 0.67, 0.67, 0.55. Expected value of 1000 × SB for the uniform P-value distribution is
\(1000\sqrt{1/{[}6(1{+}10,000){]}}{=}4.08\)
⁠.

Open in new tab

The second set of simulations was designed to evaluate power utilizing the population LD derived from an actual set of human short tandem repeat (STR) polymorphisms, described in Rosenberg  et al. (2002). We took 30 STR loci from chromosome 1, using a combined sample of 217 Middle-East and European individuals, and identified seven pairs of loci in LD by an exact test (Zaykin  et al. 1995). The resulting set of loci used for these simulations had 4–6 alleles after rare alleles were grouped together. Two-locus counts of these data were further used to set the population frequencies. These fixed population frequencies were used to obtain multinomial samples of individuals for each of the simulations. Results of these simulations are shown in Table 9. The permutational (“exact”) version of the correlation-based tests, Tp was included as well. The fit to the null (linkage equilibrium) distribution follows the same pattern found in the previous simulations—the simple approximation T2 shows a better fit than other nonexact tests. The power values are found to be similar in all cases.

TABLE 9

Human diversity panel results

Locus pair
n
T2
T1
S2
Tp
Power
15/16500.7850.7680.7300.780
9/161500.8700.8610.8570.863
19a/231500.8820.8740.8740.880
11/23a1500.8140.8050.7910.809
5/121500.7750.7620.7900.765
23a/251500.9570.9550.9520.956
21/261000.8480.8380.8700.842
Type-I error
15/16500.0500.0440.0430.044
9/161500.0530.0470.0440.047
19a/231500.0500.0470.0470.050
11/23a1500.0510.0470.0470.050
5/121500.0510.0470.0480.050
23a/251500.0480.0450.0460.047
21/261000.0510.0480.0480.049
1000 × SB
15/165018.925.326.63.5
9/161503.47.87.92.9
19a/231502.86.76.94.3
11/23a1505.19.09.12.7
5/121505.19.69.14.2
23a/251504.77.68.42.6
21/26
100
10.9
14.9
14.9
3.4
Locus pair
n
T2
T1
S2
Tp
Power
15/16500.7850.7680.7300.780
9/161500.8700.8610.8570.863
19a/231500.8820.8740.8740.880
11/23a1500.8140.8050.7910.809
5/121500.7750.7620.7900.765
23a/251500.9570.9550.9520.956
21/261000.8480.8380.8700.842
Type-I error
15/16500.0500.0440.0430.044
9/161500.0530.0470.0440.047
19a/231500.0500.0470.0470.050
11/23a1500.0510.0470.0470.050
5/121500.0510.0470.0480.050
23a/251500.0480.0450.0460.047
21/261000.0510.0480.0480.049
1000 × SB
15/165018.925.326.63.5
9/161503.47.87.92.9
19a/231502.86.76.94.3
11/23a1505.19.09.12.7
5/121505.19.69.14.2
23a/251504.77.68.42.6
21/26
100
10.9
14.9
14.9
3.4

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}10,000){]}}{=}4.08\)
⁠. Locus abbreviations: 5, ATA47D07; 9, GATA26G09; 11, GATA109; 12, GATA6A05; 15, ATA25E07; 16, ATA42G12; 19, GGAA5F09; 21, ATA4E02; 23, GATA48B01; 25, GATA4H09; 26, ATA29C07.

a

Loci in HWD.

Open in new tab
TABLE 9

Human diversity panel results

Locus pair
n
T2
T1
S2
Tp
Power
15/16500.7850.7680.7300.780
9/161500.8700.8610.8570.863
19a/231500.8820.8740.8740.880
11/23a1500.8140.8050.7910.809
5/121500.7750.7620.7900.765
23a/251500.9570.9550.9520.956
21/261000.8480.8380.8700.842
Type-I error
15/16500.0500.0440.0430.044
9/161500.0530.0470.0440.047
19a/231500.0500.0470.0470.050
11/23a1500.0510.0470.0470.050
5/121500.0510.0470.0480.050
23a/251500.0480.0450.0460.047
21/261000.0510.0480.0480.049
1000 × SB
15/165018.925.326.63.5
9/161503.47.87.92.9
19a/231502.86.76.94.3
11/23a1505.19.09.12.7
5/121505.19.69.14.2
23a/251504.77.68.42.6
21/26
100
10.9
14.9
14.9
3.4
Locus pair
n
T2
T1
S2
Tp
Power
15/16500.7850.7680.7300.780
9/161500.8700.8610.8570.863
19a/231500.8820.8740.8740.880
11/23a1500.8140.8050.7910.809
5/121500.7750.7620.7900.765
23a/251500.9570.9550.9520.956
21/261000.8480.8380.8700.842
Type-I error
15/16500.0500.0440.0430.044
9/161500.0530.0470.0440.047
19a/231500.0500.0470.0470.050
11/23a1500.0510.0470.0470.050
5/121500.0510.0470.0480.050
23a/251500.0480.0450.0460.047
21/261000.0510.0480.0480.049
1000 × SB
15/165018.925.326.63.5
9/161503.47.87.92.9
19a/231502.86.76.94.3
11/23a1505.19.09.12.7
5/121505.19.69.14.2
23a/251504.77.68.42.6
21/26
100
10.9
14.9
14.9
3.4

Expected value of 1000 × SB for the uniform P-value distribution is

\(1000\sqrt{1/{[}6(1{+}10,000){]}}{=}4.08\)
⁠. Locus abbreviations: 5, ATA47D07; 9, GATA26G09; 11, GATA109; 12, GATA6A05; 15, ATA25E07; 16, ATA42G12; 19, GGAA5F09; 21, ATA4E02; 23, GATA48B01; 25, GATA4H09; 26, ATA29C07.

a

Loci in HWD.

Open in new tab

Correspondence between approximations and the exact test for the total correlation:

Overall, we found an excellent agreement between P-values provided by either of the approximations (T1, T2) and the exact P-value given by the test Tp.

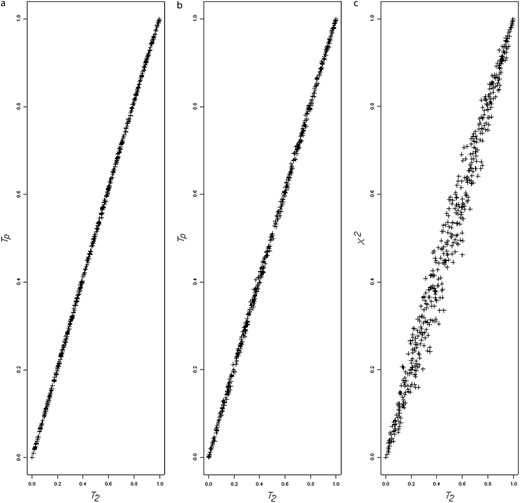
Figure 1, a and b, shows a very close P-value correspondence between T2 and the its exact version, Tp. Figure 1a plots the T2  P-values against the Tp  P-values using the subset of simulations used to produce Table 1 (N = 100). Figure 1b is a similar plot for the unknown haplotype phase data (locus pairs 11 and 23 from Table 9). For comparison, Figure 1c plots T2  P-values against those obtained by Pearson's chi-square test (N = 100, data from Table 1 simulations). There is no similar correspondence, which indicates that the two statistics are capturing somewhat different aspects of sample associations.

Figure 1.—
(a) Plots of T2  P-values against the Tp  P-values for the known haplotype phase simulations. (b) Plots of T2  P-values against the Tp  P-values for the unknown haplotype phase simulations. (c) Plots of T2  P-values against Pearson's χ2  P-values for the known haplotype phase simulations.
Open in new tabDownload slide

(a) Plots of T2  P-values against the Tp  P-values for the known haplotype phase simulations. (b) Plots of T2  P-values against the Tp  P-values for the unknown haplotype phase simulations. (c) Plots of T2  P-values against Pearson's χ2  P-values for the known haplotype phase simulations.

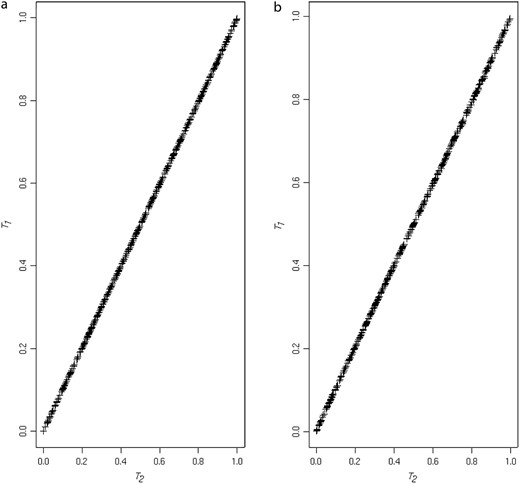
Figure 2 shows the correspondence between the two correlation-based test approximations, T1 and T2. Figure 2a illustrates the correspondence for the known haplotype phase case (N = 100; data for Table 1). Figure 2b illustrates a similar correspondence between the P-values for the unknown haplotype phase case (data from simulations to produce “setting I” in Table 8).

Figure 2.—
(a) Plots of T2  P-values against T1  P-values for the known haplotype phase simulations. (b) Plots of T2  P-values against T1  P-values for the unknown haplotype phase simulations.
Open in new tabDownload slide

(a) Plots of T2  P-values against T1  P-values for the known haplotype phase simulations. (b) Plots of T2  P-values against T1  P-values for the unknown haplotype phase simulations.

Due to closeness of P-values resulting from the T1 and the T2 tests, and much greater simplicity of the T2-statistic computation, we recommend its usage over the test based on T1.

DISCUSSION

We introduce correlation-based testing for linkage disequilibrium with multiple alleles. Following earlier work by Weir (1979) and Schaid (2004) we adopt the usage of the composite LD that provides robust inference even under conditions of high deviations from HWE. Simulations confirm that the test maintains the proper error rate even when the HWD reaches its maximum value for some of the genotypes. Our approach provides several advantages. The behavior of the proposed method under the hypothesis of no association is found to be consistently closer to the expected than that of other “nonexact” tests included in this study. Values of the statistic SB that we introduced for evaluation of the null distribution of the studied test statistics show that in 35 of 38 experiments, the approximation T2 was closer to its null expected value than the chi-square statistic (Tables 1–9). Power evaluations suggest that the correlation-based tests provide higher power than other tests under the alternatives where associations are present among multiple pairs of alleles (Tables 4–6). The novelty and advantages of our approach also include tractability of the corresponding test statistic, simplicity, and high speed of computations. The relation of the sum of squared LD correlations to chi-square extends the well-known relation for the two-allele case and thus may have implications for the design of genetic association studies. Good power properties of the test based on a simple statistic

\(T_{2}{=}(k{-}1)(m{-}1)n{\bar{r}}^{2}\)
give justification for usage of the average correlation to characterize and compare multiallelic LD in various settings, including estimation of the effective population size (Waples 2006) and fine mapping of genetic traits, where LD coefficients could be compared between samples with and without a specific disease (Nielsen  et al. 2004; Zaykin  et al. 2006). Further work may include investigation of confidence intervals for R2, on the basis of the proposed chi-square approximation.

Although the method is motivated by testing the LD, the test provides high power when used to detect heterogeneity among samples in contingency tables. For example, the correlation-based test can be used to compare allele or genotype frequencies (columns) between samples from several populations, represented by rows in a contingency table. In this setting, the power is very similar to the power of common tests such as Pearson's chi-square and Fisher's exact test. Further study may be required to fully investigate properties of this test as a general purpose test for detecting interactions and heterogeneity in contingency tables.

A computer program implementing the methods described here is available at (http://www.niehs.nih.gov/research/atniehs/labs/bb/staff/zaykin/rxc.cfm) or by a request to D.V.Z. The provided implementation computes average correlations with the corresponding P-values on the basis of the T2 statistic, using multilocus genotype data. For those P-values that fall below a user-specified threshold, a Monte Carlo P-value is reported as well. This approach allows rapid computations for large collections of loci. Correlation-based tests for contingency tables are implemented as well.

APPENDIX A

We denote the km × 1 vectors of population and sample frequencies by P and
\(\mathbf{\mathrm{{\tilde{P}}}}\)
⁠; the elements of
\(\mathbf{\mathrm{{\tilde{P}}}}\)
are the observed haplotype frequencies,
\({\tilde{p}}_{ij}{=}n_{ij}/N\)
⁠. Under the null hypothesis, H0: P = P0, we have that
\(\sqrt{N}(\mathbf{\mathrm{{\tilde{P}}}}{-}\mathbf{\mathrm{P}}_{0})\)
converges in distribution to a multivariate normal. Row and column frequencies for the table of haplotype frequencies correspond to the vectors of allele frequencies at the two loci: p, {p1, … , pk}T; q, {q1, … , qm}T. For complete absence of linkage disequilibrium, the vector of frequencies is a (km × 1) Kronecker product,
\[\mathbf{\mathrm{P}}_{0}{=}\mathbf{\mathrm{p}}\,{\otimes}\,\mathbf{\mathrm{q}}{=}{\{}p_{1}q_{1},{\,}p_{1}q_{2},{\ldots},p_{i}q_{j},{\ldots},p_{k}q_{m}{\}}^{T}\]
and the vector of expected (equilibrium) sample frequencies is based on sample values
\[\mathbf{\mathrm{\mathrm{{\tilde{P}}}}}_{0}{=}{\{}{\tilde{p}}_{1}{\tilde{q}}_{1},{\tilde{p}}_{1}{\tilde{q}}_{2},{\ldots},{\tilde{p}}_{i}{\tilde{q}}_{j},{\ldots},{\tilde{p}}_{k}{\tilde{q}}_{m}\mathrm{{\}}}^{T}.\]
Under H0, the covariance matrix of
\(\mathbf{\mathrm{{\tilde{P}}}}\)
is
\[\mathrm{Var}(\mathbf{\mathrm{{\tilde{P}}}}){=}\frac{1}{N}(\mathrm{diag}(\mathbf{\mathrm{P}}_{0}){-}\mathbf{\mathrm{P}}_{0}\mathbf{\mathrm{P}}_{0}^{T}),\]
and the variance of
\((\mathbf{\mathrm{{\tilde{P}}}}{-}\mathbf{\mathrm{{\tilde{P}}}}_{0})\)
is
\[\mathrm{Var}(\mathbf{\mathrm{{\tilde{P}}}}{-}\mathbf{\mathrm{{\tilde{P}}}}_{0}){=}\frac{1}{N}(\mathrm{diag}(\mathbf{\mathrm{p}}){-}\mathbf{\mathrm{pp}}^{T}){\otimes}(\mathrm{diag}(\mathbf{\mathrm{q}}){-}\mathbf{\mathrm{qq}}^{T})\]
(Holt  et al. 1980). The contingency table Pearson's chi-square statistic is
\[X^{2}{=}N{{\sum}_{i{=}1}^{k}}{{\sum}_{j{=}1}^{m}}\frac{({\tilde{p}}_{ij}{-}{\tilde{p}}_{i}{\tilde{q}}_{j})^{2}}{{\tilde{p}}_{i}{\tilde{q}}_{j}}.\]
(A1)
Denote
\begin{eqnarray*}&&\mathbf{\mathrm{V}}_{P}{=}\mathrm{diag}(\mathbf{\mathrm{P}}_{0}){-}\mathbf{\mathrm{P}}_{0}\mathbf{\mathrm{P}}_{0}^{T}\\&&\mathbf{\mathrm{V}}{=}(\mathrm{diag}(\mathbf{\mathrm{p}}){-}\mathbf{\mathrm{pp}}^{T}){\otimes}(\mathrm{diag}(\mathbf{\mathrm{q}}){-}\mathbf{\mathrm{qq}}^{T})\\&&\mathbf{{\Gamma}}{=}\mathrm{diag}\left[{\{}1/\sqrt{{\tilde{p}}_{i}}{\}}{\otimes}{\{}1/\sqrt{{\tilde{q}}_{i}}{\}}\right]\\&&\mathbf{{\Psi}}{=}\mathrm{diag}\left[{\{}1/\sqrt{{\tilde{p}}_{i}(1{-}{\tilde{p}}_{i})}{\}}{\otimes}{\{}1/\sqrt{{\tilde{q}}_{i}(1{-}{\tilde{q}}_{i})}{\}}\right]\\&&\mathbf{\mathrm{Z}}{=}\mathbf{{\Gamma}}(\mathbf{\mathrm{{\tilde{P}}}}{-}\mathbf{\mathrm{{\tilde{P}}}}_{0})\\&&\mathbf{\mathrm{R}}{=}\mathbf{{\Psi}}(\mathbf{\mathrm{{\tilde{P}}}}{-}\mathbf{\mathrm{{\tilde{P}}}}_{0}).\end{eqnarray*}
The notation {·} above denotes vectors; e.g.,
\({\{}1/\sqrt{p_{i}}{\}}{\equiv}{\{}1/\sqrt{p_{1}},{\ldots},1/\sqrt{p_{k}}{\}}\)
⁠. The elements of the vectors Z and R are
\[\mathbf{\mathrm{Z}}{=}\left\{\frac{{\tilde{p}}_{ij}{-}{\hat{p}}_{i}{\hat{q}}_{j}}{\sqrt{{\tilde{p}}_{i}{\tilde{q}}_{j}}}\right\}\]
(A2)
\[\mathbf{\mathrm{R}}{=}\left\{\frac{{\tilde{p}}_{ij}{-}{\tilde{p}}_{i}{\tilde{q}}_{j}}{\sqrt{{\tilde{p}}_{i}(1{-}{\tilde{p}}_{i}){\tilde{q}}_{j}(1{-}{\tilde{q}}_{i})}}\right\}.\]
(A3)
The elements of R are sample correlations for each pair of alleles, and
\(\mathbf{\mathrm{R}}^{T}\mathbf{\mathrm{R}}{=}{\sum}_{i,j}r_{ij}^{2}\)
is the sum of squared correlations for the entire table.
Pearson's X2 in (A1) can be expressed differently, using either the vector of the chi-square contributions, Z, or the vector of correlations, R,
\[\frac{1}{N}X^{2}{=}\mathbf{\mathrm{R}}^{T}(\mathbf{\mathrm{{\Psi}{\tilde{V}}}}^{{-}}\mathbf{{\Psi}})\mathbf{\mathrm{R}}\]
(A4)
\[{=}\mathbf{\mathrm{Z}}^{T}(\mathbf{\mathrm{{\Gamma}{\tilde{V}}}}^{{-}}\mathbf{{\Gamma}})\mathbf{\mathrm{Z}}\]
(A5)
\[{=}\mathbf{\mathrm{Z}}^{T}\mathbf{\mathrm{Z}},\]
(A6)
where V− denotes a generalized inverse of V. The reduction to a simple sum was given by Pearson (1922).
Our primary interest is in the approximate distribution of RTR. For any multivariate normal vector Z* with covariance matrix V*, the distribution of (Z*)TZ* is that of
\({\sum}_{i}\mathrm{{\lambda}}_{i}\mathrm{{\chi}}_{i}^{2}\)
⁠, where λi denote the nonzero eigenvalues of V* and
\(\mathrm{{\chi}}_{i}^{2}\)
are the 1-d.f. chi-square variables (Box 1954). The asymptotic covariance matrix of
\(\sqrt{N}\mathbf{\mathrm{Z}}\)
is idempotent with all (k–1)(m–1) nonzero eigenvalues being equal to 1. Hence, the sum of
\(NZ_{ij}^{2}\)
⁠, that is,
\((\sqrt{N}\mathbf{\mathrm{Z}}^{T})(\sqrt{N}\mathbf{\mathrm{Z}})\)
⁠, has an asymptotic χ2-distribution. In contrast to
\((\mathbf{\mathrm{{\Gamma}V{\Gamma}}})\)
⁠, the matrix
\((\mathbf{\mathrm{{\Psi}V{\Psi}}})\)
with (k–1)(m–1) positive eigenvalues is not idempotent. Therefore, NRTR does not have an asymptotic χ2-distribution. Box (1954) suggested that the distribution of weighted chi-square variables,
\({\sum}w_{i}\mathrm{{\chi}}_{(v_{i})}^{2}\)
⁠, where each chi square is with the degrees of freedom vi, can be approximated by a scaled chi-square distribution,
\(\mathrm{{\sigma}{\chi}}_{(d)}^{2}\)
⁠, where
\[\mathrm{{\sigma}}{=}\frac{{\sum}v_{i}w_{i}^{2}}{{\sum}v_{i}w_{i}}\]
(A7)
\[d{=}\frac{({\sum}v_{i}w_{i})^{2}}{{\sum}v_{i}w_{i}^{2}}.\]
(A8)
The degrees of freedom d need not be integral. In the case of a sum of correlations, all vi = 1, and the weights are computed from the eigenvalues of
\[\mathbf{\mathrm{V}}_{R}{=}(\mathbf{\mathrm{{\Psi}{\tilde{V}}{\Psi}}}).\]
(A9)
Since only the sums of eigenvalues or of their squares are needed, and not the eigenvalues themselves, the computations simplify substantially:
\[{\sum}w_{i}{=}\mathrm{trace}(\mathbf{\mathrm{V}}_{R}){=}km\]
(A10)
\[{\sum}w_{i}^{2}\,{=}\mathrm{trace}(\mathbf{\mathrm{V}}_{R}\mathbf{\mathrm{V}}_{R}).\]
(A11)
This makes use of the fact that eigenvalues of a squared matrix are given by squared eigenvalues of that matrix and that the trace of a symmetric matrix is given by the sum of its eigenvalues. Therefore, for our first scaled chi-square approximation we have
\[\frac{N\mathbf{\mathrm{R}}^{T}\mathbf{\mathrm{R}}}{\mathrm{{\sigma}}}{\mathrm{{\sim}}^{\mathrm{app}}}\mathrm{{\chi}}_{(d)}^{2},\]
(A12)
where
\({``}{\mathrm{{\sim}}^{\mathrm{app}}}{\textquotedblright}\)
stands for “approximately distributed” and
\[\mathrm{{\sigma}}{=}\frac{\mathrm{trace}(\mathbf{\mathrm{V}}_{R}\mathbf{\mathrm{V}}_{R})}{km}\]
(A13)
\[d{=}\frac{(km)^{2}}{\mathrm{trace}(\mathbf{\mathrm{V}}_{R}\mathbf{\mathrm{V}}_{R})}.\]
(A14)
In the second and much simpler approximation, we set the degrees of freedom equal to (k – 1)(m – 1), which is the number of nonredundant disequilibrium coefficients, Dij = pij – piqj, and note the expected values
\[\mathcal{E}(N\mathbf{\mathrm{R}}^{T}\mathbf{\mathrm{R}}){=}N\frac{km}{N}{=}km\]
\[\mathcal{E}(\mathrm{{\sigma}}\mathrm{{\chi}}_{(d)}^{2}){=}\mathrm{{\sigma}}d\]
\[\mathrm{Var}(\mathrm{{\sigma}}\mathrm{{\chi}}_{(d)}^{2}){=}\left[E(\mathrm{{\chi}}_{(d)}^{2})\right]^{2}\frac{2}{d}.\]
(A15)
By matching moments, the scale parameter is found to be
\(\mathrm{{\sigma}}{=}km/{[}(k{-}1)(m{-}1){]}\)
⁠. Thus, we obtain our second approximate distribution as
\[\frac{N(k{-}1)(m{-}1)}{km}\mathbf{\mathrm{R}}^{T}\mathbf{\mathrm{R}}{\mathrm{{\sim}}^{\mathrm{app}}}\mathrm{{\chi}}_{(k{-}1)(m{-}1)}^{2}.\]
(A16)
Note that RTR/(km) is just the average squared correlation. Waples (2006) noted that approximately, the distribution of such a coefficient might be a chi square and that with k alleles per locus, the number of independent comparisons (and thus the degrees of freedom) for a comparison of two loci should be (k – 1)2. Nevertheless, he did not provide a distribution explicitly.

APPENDIX B

Tables of population joint frequencies (pij) to provide a specified amount of association (measured by D′) for the power study.

TABLE B1

The 4 × 3 table of joint frequencies with the corresponding level of association

pij\D′
Sum
0.0871\0.50.1567\0.50.1134\−0.50.357
0.0133\−0.50.0240\−0.50.1697\0.50.207
0.0107\−0.50.0192\−0.50.1359\0.50.166
0.0174\−0.50.0313\−0.50.2213\0.50.270
Sum
0.128
0.231
0.640
pij\D′
Sum
0.0871\0.50.1567\0.50.1134\−0.50.357
0.0133\−0.50.0240\−0.50.1697\0.50.207
0.0107\−0.50.0192\−0.50.1359\0.50.166
0.0174\−0.50.0313\−0.50.2213\0.50.270
Sum
0.128
0.231
0.640

Absolute values of D′ for this set of simulations are set to be ±0.5.

Open in new tab
TABLE B1

The 4 × 3 table of joint frequencies with the corresponding level of association

pij\D′
Sum
0.0871\0.50.1567\0.50.1134\−0.50.357
0.0133\−0.50.0240\−0.50.1697\0.50.207
0.0107\−0.50.0192\−0.50.1359\0.50.166
0.0174\−0.50.0313\−0.50.2213\0.50.270
Sum
0.128
0.231
0.640
pij\D′
Sum
0.0871\0.50.1567\0.50.1134\−0.50.357
0.0133\−0.50.0240\−0.50.1697\0.50.207
0.0107\−0.50.0192\−0.50.1359\0.50.166
0.0174\−0.50.0313\−0.50.2213\0.50.270
Sum
0.128
0.231
0.640

Absolute values of D′ for this set of simulations are set to be ±0.5.

Open in new tab
TABLE B2

The 4 × 3 table of joint frequencies with the corresponding level of association

pij\D′
Sum
0.0844\0.50.0114\−0.50.0106\−0.50.106
0.1390\−0.50.1534\0.50.1437\0.50.436
0.0803\0.50.0108\−0.50.0101\−0.50.101
0.2825\0.50.0381\−0.50.0356\−0.50.356
Sum
0.586
0.214
0.200
pij\D′
Sum
0.0844\0.50.0114\−0.50.0106\−0.50.106
0.1390\−0.50.1534\0.50.1437\0.50.436
0.0803\0.50.0108\−0.50.0101\−0.50.101
0.2825\0.50.0381\−0.50.0356\−0.50.356
Sum
0.586
0.214
0.200

Absolute values of D′ for this set of simulations are set to be ±0.5.

Open in new tab
TABLE B2

The 4 × 3 table of joint frequencies with the corresponding level of association

pij\D′
Sum
0.0844\0.50.0114\−0.50.0106\−0.50.106
0.1390\−0.50.1534\0.50.1437\0.50.436
0.0803\0.50.0108\−0.50.0101\−0.50.101
0.2825\0.50.0381\−0.50.0356\−0.50.356
Sum
0.586
0.214
0.200
pij\D′
Sum
0.0844\0.50.0114\−0.50.0106\−0.50.106
0.1390\−0.50.1534\0.50.1437\0.50.436
0.0803\0.50.0108\−0.50.0101\−0.50.101
0.2825\0.50.0381\−0.50.0356\−0.50.356
Sum
0.586
0.214
0.200

Absolute values of D′ for this set of simulations are set to be ±0.5.

Open in new tab
TABLE B3

The 5 × 5 table of joint frequencies with the corresponding level of association, pij\D′

pij\D′
Sum
0.1183\0.200.0233\−0.200.0434\−0.210.0529\−0.200.0385\−0.200.277
0.0233\−0.200.0086\−0.200.0365\0.200.0196\−0.200.0142\−0.200.102
0.0228\−0.200.0084\−0.200.0357\0.200.0192\−0.200.0139\−0.200.100
0.0399\−0.190.0147\−0.200.0275\−0.200.0335\−0.200.0592\0.200.175
0.0791\−0.190.0502\0.200.0545\−0.200.1143\0.200.0483\−0.200.346
Sum
0.284
0.105
0.198
0.239
0.174
pij\D′
Sum
0.1183\0.200.0233\−0.200.0434\−0.210.0529\−0.200.0385\−0.200.277
0.0233\−0.200.0086\−0.200.0365\0.200.0196\−0.200.0142\−0.200.102
0.0228\−0.200.0084\−0.200.0357\0.200.0192\−0.200.0139\−0.200.100
0.0399\−0.190.0147\−0.200.0275\−0.200.0335\−0.200.0592\0.200.175
0.0791\−0.190.0502\0.200.0545\−0.200.1143\0.200.0483\−0.200.346
Sum
0.284
0.105
0.198
0.239
0.174

Absolute values of D′ for this set of simulations are set to be in the range 0.19–0.21.

Open in new tab
TABLE B3

The 5 × 5 table of joint frequencies with the corresponding level of association, pij\D′

pij\D′
Sum
0.1183\0.200.0233\−0.200.0434\−0.210.0529\−0.200.0385\−0.200.277
0.0233\−0.200.0086\−0.200.0365\0.200.0196\−0.200.0142\−0.200.102
0.0228\−0.200.0084\−0.200.0357\0.200.0192\−0.200.0139\−0.200.100
0.0399\−0.190.0147\−0.200.0275\−0.200.0335\−0.200.0592\0.200.175
0.0791\−0.190.0502\0.200.0545\−0.200.1143\0.200.0483\−0.200.346
Sum
0.284
0.105
0.198
0.239
0.174
pij\D′
Sum
0.1183\0.200.0233\−0.200.0434\−0.210.0529\−0.200.0385\−0.200.277
0.0233\−0.200.0086\−0.200.0365\0.200.0196\−0.200.0142\−0.200.102
0.0228\−0.200.0084\−0.200.0357\0.200.0192\−0.200.0139\−0.200.100
0.0399\−0.190.0147\−0.200.0275\−0.200.0335\−0.200.0592\0.200.175
0.0791\−0.190.0502\0.200.0545\−0.200.1143\0.200.0483\−0.200.346
Sum
0.284
0.105
0.198
0.239
0.174

Absolute values of D′ for this set of simulations are set to be in the range 0.19–0.21.

Open in new tab

Footnotes

Communicating editor: A. D. Long

Acknowledgement

Shyamal Peddada and David Umbach provided useful discussion. Noah Rosenberg provided STR genotypes for deriving data sets used in the simulation study. Daniel Schaid and Jason Sinnwell provided a program implementing Schaid's S2 test. This research was supported in part by the Intramural Research Program of the National Institutes of Health (NIH), National Institute of Environmental Health Sciences, and by NIH GM 07591.

References

Boos, D. D., and J. Zhang,

2000
Monte Carlo evaluation of resampling-based hypothesis tests.
J. Am. Stat. Assoc.
 
95
:  
486
–492.

Crossref
Search ADS
 

Box, G. E. P.,

1954
Some theorems on quadratic forms applied in the study of analysis of variance problems, II. Effect of inequality of variance in the two-way classification.
Ann. Math. Stat.
 
25
:  
290
–302.

Crossref
Search ADS
 

Cressie, N., and T. R. C. Read,

1984
Multinomial goodness-of-fit tests.
J. R. Stat. Soc. B
 
46
:  
440
–464.

Evett, I. W., and B. S. Weir,

1998
 Interpreting DNA Evidence. Sinauer Associates, Sunderland, MA.

Excoffier, L., and M. Slatkin,

1995
Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population.
Mol. Biol. Evol.
 
12
:  
921
–927.

PubMed
 

Fienberg, S. E.,

1979
The use of chi-squared statistics for categorical data problems J.
R. Stat. Soc. B
 
41
:  
54
–64.

Hill, W. G.,

1974
Estimation of linkage disequilibrium in randomly mating populations.
Heredity
 
33
:  
229
–232.

Crossref
Search ADS
PubMed
 

Hill, W. G.,

1975
Tests for association of gene frequencies at several loci in random mating diploid populations.
Biometrics
 
31
:  
881
–888.

Crossref
Search ADS
PubMed
 

Hedrick, P. W.,

1987
Gametic disequilibrium measures: proceed with caution.
Genetics
 
117
:  
331
–341.

Crossref
Search ADS
PubMed
 

Ipsen, J., and N. K. Jerne,

1944
Graphical evaluation of the distribution of small experimental series.
Acta Pathol. Microbiol. Scand.
 
21
:  
343
–361.

Kalinowski, S. T., and P. W. Hedrick,

2000
Estimation of linkage disequilibrium for loci with multiple alleles: basic approach and an application using data from bighorn sheep.
Heredity
 
87
:  
698
–708.

Karlin, S., and A. Piazza,

1981
Statistical methods for assessing linkage disequilibrium at the HLA-A, B, C loci.
Ann. Hum. Genet.
 
45
:  
79
–94.

Crossref
Search ADS
PubMed
 

Holt, D., A. J. Scott and P. D. Ewings,

1980
Chi-squared tests with survey data.
J. R. Stat. Soc. A
 
143
:  
303
–320.

Crossref
Search ADS
 

International  HapMap  Consortium,

2003
The International HapMap Project.
Nature.
 
426
:  
789
–796.

Crossref
Search ADS
PubMed
 

Larntz, L.,

1978
Small-sample comparisons of exact levels for chi-squared goodness-of-fit statistics.
J. Am. Stat. Assoc.
 
73
:  
253
–263.

Crossref
Search ADS
 

Lewontin, R. C.,

1964
The interaction of selection and linkage. I. General considerations; heterotic models.
Genetics
 
49
:  
49
–67.

Crossref
Search ADS
PubMed
 

Lewontin, R. C.,

1974
 The Genetic Basis of Evolutionary Change. Columbia University Press, New York.

Nielsen, D. M., M. G. Ehm, D. V. Zaykin and B. S. Weir,

2004
Effect of two-and three-locus linkage disequilibrium on the power to detect marker/phenotype associations.
Genetics
 
168
:  
1029
–1040.

Crossref
Search ADS
PubMed
 

Oden, N. L.,

1991
Allocation of effort in Monte Carlo simulation for power of permutation tests.
J. Am. Stat. Assoc.
 
86
:  
1074
–1076.

Crossref
Search ADS
 

Pearson, K.,

1922
On the χ2 test of goodness of fit.
Biometrika
 
14
:  
186
–191.

Pritchard, J. K., and M. Przeworski,

2001
Linkage disequilibrium in humans: models and data.
Am. J. Hum. Genet.
 
69
:  
1
–14.

Crossref
Search ADS
PubMed
 

Rosenberg, N. A., J. K. Pritchard, J. L. Weber, H. M. Cann, K. K. Kidd  et al.,

2002
Genetic structure of human populations.
Science
 
298
:  
2981
–2985.

Schaid, D. J.,

2004
Linkage disequilibrium testing when linkage phase is unknown.
Genetics
 
166
:  
505
–512.

Crossref
Search ADS
PubMed
 

Searle, S. R.,

1971
 Linear Models. John Wiley & Sons, New York.

Slatkin, M.,

1994
Linkage disequilibrium in growing and stable populations.
Genetics
 
137
:  
331
–336.

Crossref
Search ADS
PubMed
 

Terwilliger, J. D., and T. Hiekkalinna,

2006
An utter refutation of the “Fundamental Theorem of the HapMap”.
Eur. J. Hum. Genet.
 
14
:  
426
–437.

Crossref
Search ADS
PubMed
 

Tishkoff, S. A., E. Dietzsch, W. Speed, A. J. Pakstis, J. R. Kidd  et al.,

1996
Global patterns of linkage disequilibrium at the CD4 locus and modern human origins.
Science
 
271
:  
1380
–1387.

Crossref
Search ADS
PubMed
 

Waples, R. S.,

2006
A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci.
Conserv. Genet.
 
7
:  
167
–184.

Crossref
Search ADS
 

Weir, B. S.,

1979
Inferences about linkage disequilibrium.
Biometrics
 
35
:  
235
–254.

Crossref
Search ADS
PubMed
 

Weir, B. S.,

1996
 Genetic Data Analysis II. Sinauer Associates, Sunderland, MA.

Weir, B. S., and C. C. Cockerham,

1978
Testing hypotheses about linkage disequilibrium with multiple alleles.
Genetics
 
88
:  
633
–642.

Crossref
Search ADS
PubMed
 

Weir, B. S., and C. C. Cockerham,

1979
Estimation of linkage disequilibrium in randomly mating populations.
Heredity
 
42
:  
105
–111.

Crossref
Search ADS
 

Weir, B. S., and C. C. Cockerham,

1989
Complete characterization of disequilibrium at two loci, pp. 86–110 in Mathematical Evolutionary Theory, edited by M. W. Feldman. Princeton University Press, Princeton, NJ.

Yamazaki, T.,

1977
The effects of overdominance on linkage in a multilocus system.
Genetics
 
86
:  
227
–236.

Crossref
Search ADS
PubMed
 

Zapata, C.,

2000
The D′ measure of overall gametic disequilibrium between pairs of multiallelic loci.
Evolution
 
54
:  
1809
–1812.

PubMed
 

Zaykin, D., L. Zhivotovsky and B. S. Weir,

1995
Exact tests for association between alleles at arbitrary numbers of loci.
Genetica
 
96
:  
169
–178.

Crossref
Search ADS
PubMed
 

Zaykin, D. V.,

2004
Bounds and normalization of the composite linkage disequilibrium coefficient.
Genet. Epidemiol.
 
27
:  
252
–257.

Crossref
Search ADS
PubMed
 

Zaykin, D. V., Z. Meng and M. G. Ehm,

2006
Contrasting linkage-disequilibrium patterns between cases and controls as a novel association-mapping method.
Am. J. Hum. Genet.
 
78
:  
737
–746.

Crossref
Search ADS
PubMed
 

Zhao, H., D. Nettleton, M. Soller and J. C. M. Dekkers,

2005
Evaluation of linkage disequilibrium measures between multi-allelic markers as predictors of linkage disequilibrium between markers and QTL.
Genet. Res.
 
86
:  
77
–87.

Crossref
Search ADS
PubMed
 

Zhao, H., D. Nettleton and J. C. M. Dekkers,

2007
Evaluation of linkage disequilibrium measures between multi-allelic markers as predictors of linkage disequilibrium between single nucleotide polymorphisms.
Genet. Res.
 
89
:  
1
–6.

Crossref
Search ADS
PubMed
 
© Genetics 2008
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://academic.oup.com/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Population and Evolutionary Genetics
Download all slides